Помощь по Теле2, тарифы, вопросы

Предельный цикл есть изолированная замкнутая кривая на фазовой плоскости, к которой в пределе при t ® ¥ стремятся все интегральные кривые. Предельный цикл представляет стационарный режим с определенной амплитудой, не зависящий от начальных условий, а определяющийся только организацией системы. Существование предельного цикла на фазовой плоскости есть основной признак автоколебательной системы. Очевидно, что при автоколебательном процессе фаза колебаний может быть любой.

Остановимся на общих характеристиках автоколебательных систем. Рассмотрим систему уравнений общего вида:

Если T (T > 0) - наименьшее число, для которого при всяком t

то изменение переменных x = x(t), y = y(t) называется периодическим изменением с периодом T.

Периодическому изменению соответствует замкнутая траектория на фазовой плоскости, и обратно: всякой замкнутой траектории соответствует бесконечное множество периодических изменений, отличающихся друг от друга выбором начала отсчета времени.

Если периодическому изменению на фазовой плоскости соответствуетизолированная замкнутая кривая, к которой с внешней и внутренней стороны приближаются (при возрастании t ) соседние траектории по спиралям, эта изолированная замкнутая траектория есть предельный цикл .

Простые примеры позволяют убедиться, что система общего вида (8.1) допускает в качестве траекторий предельные циклы.

Например, для системы

(8.2)

траектория является предельным циклом. Его параметрические уравнения будут:

а уравнения всех других фазовых траекторий запишутся в виде:

.

Значениям постоянной интегрирования С > 0 соответствуют фазовые траектории, накручивающиеся на предельный цикл изнутри (при t ®¥), а значениям –1< C <0 траектории, накручивающиеся снаружи.

Предельный цикл называетсяустойчивым, если существует такая область на фазовой плоскости, содержащая этот предельныйцикл, - окрестность e, что все фазовые траектории, начинающиеся в окрестности e, асимптотически при t ® ¥ приближаются кпредельному циклу.

Если же, наоборот, в любой сколь угодно малой окрестности e предельного цикла существует по крайней мере одна фазовая траектория, не приближающаяся к предельному циклупри t ® ¥, то такой предельный цикл называется неустойчивым. Такие циклы разделяют области влияния (бассейны) разных притягивающих множеств.

На рис. 8.2 изображены устойчивый предельный цикл (а ) и неустойчивые (б ) и (в ).

Неустойчивые предельные циклы, подобные изображенному на рис. 8.2 б , такие, что все траектории с одной стороны (например, изнутри) приближаются к ним, а с другой стороны (например, извне) удаляются от них при t ® ¥, называют «полуустойчивыми» или двойными. Последнее название связано с тем, что обычно такие циклы при подходящем изменении параметра системы расщепляются на два, один из которых устойчив, а другой неустойчив.

А.М. Ляпунов показал, что для исследования устойчивости периодического движения x = j(t ), y = y(t ) можно идти по пути линеаризации уравнений, подобно тому, как мы это делали при исследовании устойчивости состояний равновесия. Если положить

подставить эти выражения в уравнения (8.1), разложить правые части этих уравнений - функции

в ряды по степеням x и h и отбросить нелинейные члены, то мы получим линейные уравнения (уравнения первого приближения) для координат возмущения x и h:

Коэффициенты в правой части:

Это система линейных дифференциальных уравнений с периодическими коэффициентами периода T , поскольку a , b , c , d суть функции от j, y - периодических функций времени с периодом T . Общий вид ее решения

Здесь - некоторые периодические функции с периодом T . От показателей и которые носят название «характеристических показателей», зависят свойства решений для отклонений от стационарного периодического решения x и h. А именно, знаки их действительных частей определяют, являются ли эти решения нарастающими или затухающими. Можно показать, что в силу автономности исходной системы (8.1) один из характеристических показателей равен нулю, а другой равен h .

где x = j(t ), y = y(t ) - любое периодическое решение, соответствующее рассматриваемому предельному циклу, T - период решения.

Таким образом, устойчивость предельного цикла (и устойчивость в смысле Ляпунова соответствующих периодических движений) определяется знаком характеристического показателя. Предельный цикл устойчив, если h < 0 и неустойчив, если h > 0. Если же h = 0, уравнения первого приближения не решают вопроса об устойчивости периодического движения.

Для нахождения предельных циклов не существует таких простых аналитических методов, как для нахождения стационарных точек и исследования их устойчивости. Однако, исследование фазовой плоскости системы позволяет ответить на вопрос, есть в данной системе предельный цикл, или нет.

Сформулируем несколько теорем, определяющих наличие предельного цикла по топологическому строению фазовой плоскости. Они могут быть полезны как при аналитическом, так и при компьютерном анализе системы.

Теорема 1. Пусть на фазовой плоскости существует область, из которой фазовые траектории не выходят, и в которой нет положений равновесия (особых точек). Тогда в этой области обязательно существует предельный цикл, причем все остальные траектории обязательно наматываются на него.

На рис. 8.3. изображена такая область G , из которой фазовые траектории не выходят. Это означает, что фазовые траектории либо входят, пересекая границу, внутрь области, либо сама граница является траекторией. Легко видеть, что такая область не может быть односвязной. Поскольку траектория наматывается на предельный цикл изнутри, это означает, что внутри этого предельного цикла на фазовой плоскости существует либо неустойчивая особая точка, либо неустойчивый предельный цикл, очевидно, не принадлежащие рассматриваемой области G .

Таким образом, если найти на фазовой плоскости такую двусвязную область, что направления фазовых траекторий на всей границе обращены внутрь этой области, то можно утверждать, что внутри этой области имеется предельный цикл.

Теорема 2. Если существует на фазовой плоскости некоторая замкнутая область, такая, что все фазовые траектории, пересекающие границу этой области, входят в нее, и внутри этой области находится неустойчивая особая точка, то в этой области обязательно имеется хотя бы один предельный цикл (рис. 8.4)

Приведем также некоторые критерии отсутствия замкнутых фазовых траекторий (в том числе предельных циклов).

1. Если в системе не существует особых точек, то в ней не может быть и замкнутых фазовых траекторий.

2. Если в системе существует только одна особая точка, отличная от узла, фокуса и центра (например, седло), то такая система не допускает замкнутых фазовых траекторий.

3. Если в системе имеются только простые особые точки, причем через все точки типа узел и фокус проходят интегральные кривые, уходящие на бесконечность, то в такой системе нет замкнутых фазовых траекторий.

В случае, если критерии 1–3 выполнены, можно с уверенностью утверждать, что в системе нет предельных циклов. Однако невыполнение этих критериев еще не позволяет сделать вывод о наличии в системе предельных циклов и, следовательно, автоколебаний.

Неустойчивый предельный цикл также может содержаться в фазовом портрете грубых систем. Однако такой предельный цикл не соответствует реальному периодическому процессу, он играет лишь роль «водораздела», по обе стороны которого траектории имеют различное поведение. Например, на рис. 8.5 представляет собой сепаратрису, отделяющую область тяготения траекторий к устойчивой особой точке, с одной стороны, и к устойчивому предельному циклу, с другой.

ЛЕКЦИЯ 8

КОЛЕБАНИЯ В БИОЛОГИЧЕСКИХ СИСТЕМАХ

Понятие автоколебаний. Изображение автоколебательной системы на фазовой плоскости. Предельные циклы. Условия существования предельных циклов. Рождение предельного цикла. Бифуркация Андронова ‑ Хопфа. Мягкое и жесткое возбуждение колебаний. Модель брюсселятор. Примеры автоколебательных моделей процессов в живых системах. Колебания в темновых процессах фотосинтеза. Автоколебания в модели гликолиза. Внутриклеточные колебания концентрации кальция. Клеточные циклы.

Для биологических систем характерно периодическое изменение различных характеристик. Период этих колебаний может быть связан с периодическими изменениями условий жизни на Земле - смена времен года, смена дня и ночи. Существуют и другие геофизические ритмы –солнечные, лунные, связанные с периодами атмосферных явлений. Геофизические и биологические ритмы сопоставлены на рис. 8.1. Но многие периодические процессы имеют частоту изменения, не связанную очевидным образом с внешними геокосмическими циклами. Это так называемые «биологические часы» различной природы, начиная от колебаний биомакромолекул, биохимических колебаний, вплоть до популяционных волн.

Внутриклеточные колебания задают эндогенные биологические ритмы, которые свойственны всем живым системам. Именно они определяют периодичность деления клеток, отмеряют время рождения и смерти живых организмов. Модели колебательных систем используются в ферментативном катализе, теории иммунитета, в теории трансмембранного ионного переноса, микробиологии и биотехнологии.

С некоторыми из типов периодических движений мы уже имели дело при рассмотрении особых точек типа центр и затухающих или нарастающих колебаний в случае устойчивого и неустойчивого фокуса. Однако «биологические часы» имеют свойство, отличающее их от рассмотренных типов колебаний - неизменность во времени периода и амплитуды таких колебаний, означающую стационарность и устойчивость колебательного режима .

Рис. 8.1. Космофизические, геофизические и биологические ритмы. Справа – шкала периодов, слева – шкала частот

В данном случае периодическое изменение величин представляет собой один из типов стационарного поведения системы. Если колебания в системе имеют постоянные период и амплитуду, устанавливаются независимо от начальных условий и поддерживаются благодаря свойствам самой системы, а не вследствие воздействия периодической силы, система называется автоколебательной .

Незатухающие колебания в таких системах устойчивы, так как отклонения от стационарного колебательного режима затухают. К классу автоколебательных систем относятся колебания в гликолизе и других метаболических системах, периодические процессы фотосинтеза, колебания концентрации кальция в клетке, колебания численности животных в популяциях и сообществах.

Предельный цикл. В фазовом пространстве такому типу поведения соответствует притягивающее множество (аттрактор), называемое предельным циклом .

Предельный цикл есть изолированная замкнутая кривая на фазовой плоскости, к которой в пределе при t ® ¥ стремятся все интегральные кривые. Предельный цикл представляет стационарный режим с определенной амплитудой, не зависящий от начальных условий, а определяющийся только организацией системы. Существование предельного цикла на фазовой плоскости есть основной признак автоколебательной системы. Очевидно, что при автоколебательном процессе фаза колебаний может быть любой.

Остановимся на общих характеристиках автоколебательных систем. Рассмотрим систему уравнений общего вида:

(8.1)

Если T (T > 0) - наименьшее число, для которого при всяком t

то изменение переменных x = x ( t ), y = y ( t ) называется периодическим изменением с периодом T.

Периодическому изменению соответствует замкнутая траектория на фазовой плоскости, и обратно: всякой замкнутой траектории соответствует бесконечное множество периодических изменений, отличающихся друг от друга выбором начала отсчета времени.

Если периодическому изменению на фазовой плоскости соответствуетизолированная замкнутая кривая, к которой с внешней и внутренней стороны приближаются (при возрастании t ) соседние траектории по спиралям, эта изолированная замкнутая траектория есть предельный цикл .

Простые примеры позволяют убедиться, что система общего вида (8.1) допускает в качестве траекторий предельные циклы.

Например, для системы

(8.2)

траектория является предельным циклом. Его параметрические уравнения будут:

а уравнения всех других фазовых траекторий запишутся в виде:

.

Значениям постоянной интегрирования С > 0 соответствуют фазовые траектории, накручивающиеся на предельный цикл изнутри (при t ® ¥ ), а значениям –1 < C < 0 траектории, накручивающиеся снаружи.

Предельный цикл называетсяустойчивым, если существует такая область на фазовой плоскости, содержащая этот предельныйцикл, - окрестность e , что все фазовые траектории, начинающиеся в окрестности e , асимптотически при t ® ¥ приближаются кпредельному циклу.

Если же, наоборот, в любой сколь угодно малой окрестности e предельного цикла существует по крайней мере одна фазовая траектория, не приближающаяся к предельному циклупри t ® ¥ , то такой предельный цикл называется неустойчивым. Такие циклы разделяют области влияния (бассейны) разных притягивающих множеств.

На рис. 8.2 изображены устойчивый предельный цикл (а ) и неустойчивые (б ) и (в ).

Неустойчивые предельные циклы, подобные изображенному на рис. 8.2 б , такие, что все траектории с одной стороны (например, изнутри) приближаются к ним, а с другой стороны (например, извне) удаляются от них при t ® ¥ , называют «полуустойчивыми» или двойными. Последнее название связано с тем, что обычно такие циклы при подходящем изменении параметра системы расщепляются на два, один из которых устойчив, а другой неустойчив.

А.М. Ляпунов показал, что для исследования устойчивости периодического движения x = j (t ), y = y (t ) можно идти по пути линеаризации уравнений, подобно тому, как мы это делали при исследовании устойчивости состояний равновесия. Если положить

подставить эти выражения в уравнения (8.1), разложить правые части этих уравнений - функции

в ряды по степеням x и h и отбросить нелинейные члены, то мы получим линейные уравнения (уравнения первого приближения) для координат возмущения x и h :

Коэффициенты в правой части:

Это система линейных дифференциальных уравнений с периодическими коэффициентами периода T , поскольку a , b , c , d суть функции от j , y - периодических функций времени с периодом T . Общий вид ее решения

Здесь - некоторые периодические функции с периодом T . От показателей и которые носят название «характеристических показателей», зависят свойства решений для отклонений от стационарного периодического решения x и h . А именно, знаки их действительных частей определяют, являются ли эти решения нарастающими или затухающими. Можно показать, что в силу автономности исходной системы (8.1) один из характеристических показателей равен нулю, а другой равен h .

где x = j (t ), y = y (t ) - любое периодическое решение, соответствующее рассматриваемому предельному циклу, T - период решения.

Таким образом, устойчивость предельного цикла (и устойчивость в смысле Ляпунова соответствующих периодических движений) определяется знаком характеристического показателя. Предельный цикл устойчив, если h < 0 и неустойчив, если h > 0. Если же h = 0, уравнения первого приближения не решают вопроса об устойчивости периодического движения.

Для нахождения предельных циклов не существует таких простых аналитических методов, как для нахождения стационарных точек и исследования их устойчивости. Однако, исследование фазовой плоскости системы позволяет ответить на вопрос, есть в данной системе предельный цикл, или нет.

Сформулируем несколько теорем, определяющих наличие предельного цикла по топологическому строению фазовой плоскости. Они могут быть полезны как при аналитическом, так и при компьютерном анализе системы.

Теорем а 1. Пусть на фазовой плоскости существует область, из которой фазовые траектории не выходят, и в которой нет положений равновесия (особых точек). Тогда в этой области обязательно существует предельный цикл, причем все остальные траектории обязательно наматываются на него.

На рис. 8.3. изображена такая область G , из которой фазовые траектории не выходят. Это означает, что фазовые траектории либо входят, пересекая границу, внутрь области, либо сама граница является траекторией. Легко видеть, что такая область не может быть односвязной. Поскольку траектория наматывается на предельный цикл изнутри, это означает, что внутри этого предельного цикла на фазовой плоскости существует либо неустойчивая особая точка, либо неустойчивый предельный цикл, очевидно, не принадлежащие рассматриваемой области G .

Таким образом, если найти на фазовой плоскости такую двусвязную область, что направления фазовых траекторий на всей границе обращены внутрь этой области, то можно утверждать, что внутри этой области имеется предельный цикл.

Теорема 2. Если существует на фазовой плоскости некоторая замкнутая область, такая, что все фазовые траектории, пересекающие границу этой области, входят в нее, и внутри этой области находится неустойчивая особая точка, то в этой области обязательно имеется хотя бы один предельный цикл (рис. 8.4)

Приведем также некоторые критерии отсутствия замкнутых фазовых траекторий (в том числе предельных циклов).

1. Если в системе не существует особых точек, то в ней не может быть и замкнутых фазовых траекторий.

2. Если в системе существует только одна особая точка, отличная от узла, фокуса и центра (например, седло), то такая система не допускает замкнутых фазовых траекторий.

3. Если в системе имеются только простые особые точки, причем через все точки типа узел и фокус проходят интегральные кривые, уходящие на бесконечность, то в такой системе нет замкнутых фазовых траекторий.

В случае, если критерии 1–3 выполнены, можно с уверенностью утверждать, что в системе нет предельных циклов. Однако невыполнение этих критериев еще не позволяет сделать вывод о наличии в системе предельных циклов и, следовательно, автоколебаний.

Неустойчивый предельный цикл также может содержаться в фазовом портрете грубых систем. Однако такой предельный цикл не соответствует реальному периодическому процессу, он играет лишь роль «водораздела», по обе стороны которого траектории имеют различное поведение. Например, на рис. 8.5 представляет собой сепаратрису, отделяющую область тяготения траекторий к устойчивой особой точке, с одной стороны, и к устойчивому предельному циклу, с другой.

Рождение предельного цикла. Бифуркация Андронова-Хопфа.

Существование предельных циклов возможно лишь в системе типа (8.1), правые части которой представлены нелинейными функциями.

На бифуркационной диаграмме 4.11 мы видели, что при пересечении оси абсцисс происходит смена устойчивости фокуса. Нулевым значениям действительной части характеристических чисел (ляпуновских показателей) соответствует особая точка типа центр. В нелинейной системе, где возникает неустойчивый фокус, при этом возможно рождение предельного цикла. Такой переход легко проследить в «модельной» системе:

(8.3)

Схематически возникновение предельного цикла в системе (8.3) изображено на фазопараметрической диаграмме на рис. 8.6.

Рис. 8.6. Закритическая (суперкритическая) бифуркация Андронова-Хопфа. Мягкое возбуждение. При с >0 возникают автоколебания, амплитуда которых растет с увеличением с .

Выполнению условия Re l 1,2 = 0, причем Im l 1,2 ¹ 0, соответствует бифуркация Андронова–Хопфа или бифуркация рождения (исчезновения) предельного цикла. Бифуркация впервые была исследована А.А. Андроновым для случая N = 2 и обобщена Е. Хопфом на системы с произвольной размерностью. (Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., Наука, 1981;Hopf E ., 1942)

Существуют два типа бифуркации Андронова–Хопфа. Только что мы рассмотрели суперкритическую бифуркацию (мягкое возбуждение автоколебаний). Возможна также субкритическая бифуркация (жесткое возбуждение автоколебаний). В этом случае при бифуркационном значении параметра устойчивый фокус теряет устойчивость из-за «влипания» в него неустойчивого предельного цикла (рис. 8.7). Фокус становится неустойчивым, а аттрактором при этом может стать предельный цикл большой амплитуды.

«Модельной» системой (см. лекция 6), описывающей рождение предельного цикла при жестком возбуждении, является система:

(8.4)

Приравняв правую часть первого уравнения нулю, получим стационарные значения r :

Ветвь r = 0 устойчива при c < 0 и неустойчива при c > 0.

При с > –1 стационарное решение - устойчивый предельный цикл.

При –1<с <0 стационарное решение - неустойчивый предельный цикл.

Рассмотрим, что произойдет, если двигаться по параметру с , начиная с отрицательных значений (Рис.8.8). Первоначально имеется единственное устойчивое стационарное состояние r = 0, колебаний нет. При c > –1 существует также устойчивый предельный цикл, но система не покидает своего устойчивого стационарного состояния. Однако после того как с становится положительным, стационарное состояние становится неустойчивым, и происходит резкий скачок к устойчивому предельному циклу. В системе начинаются колебания сразу большой амплитуды. Если двигаться от положительных значений с к отрицательным, колебания большой амплитуды сохраняются до тех пор, пока с не станет меньше –1, а затем внезапно исчезнут. Таким образом при –1 < с < 0 могут существовать два различных типа поведения. Какой из них реализуется, зависит от предыстории системы. Такой феномен называется эффектом гистерезиса.

При увеличении параметра с и его переходе через ноль скачком возникают устойчивые автоколебания конечной амплитуды и частоты. Для промежуточных значений параметра с существуют два типа устойчивого поведения (два аттрактора) - устойчивое стационарное состояниеи устойчивый предельный цикл.

Винфри (Winfree A . T . ) назвал области, в которых возможны два режима: устойчивая точка покоя и предельный цикл, ­- черной дырой (рис. 8.8 б) . В этой области параметров можно так приложить возмущение к колебательной системе, что она попадет в область притяжения точки покоя, что приведет к прекращению колебаний. В частности, это показано для уравнений Ходжкина–Хаксли, моделирующих проведение нервного импульса (см. ниже).

Брюсселятор. Простейшим классическим примером существования автоколебаний в системе химических реакций является тримолекулярная модель «Брюсселятор», предложенная в Брюсселе Пригожиным и Лефевром (1965). Основной целью при изучении этой модели было установление качественных типов поведения, совместимых с фундаментальными законами химической и биологической кинетики.

В этом смысле блюсселятор играет роль базовой модели, такую же как гармонический осциллятор в физике, или модели Вольтерра в динамике популяций. Во 2-й части лекций мы остановимся на пространственно‑временных свойствах распределенной системы, локальным элементом которой является брюсселятор. Здесь мы рассмотрим свойства брюсселятора как автоколебательной системы.

Брюсселятор содержит простейшую реализацию кубической нелинейности посредством химической реакции

2X + Y ® 3X (8.5)

Хотя тримолекулярная стадия в химической кинетике не столь распространена, как бимолекулярные процессы, выражения для скорости ряда биохимических реакций в определенных случаях можно свести к кубическому виду. В качестве примера приведем следующую последовательность ферментативных реакций:

X + E ® EX

EX + Y ® XY

EXY + X ® EX 2 Y

Здесь предполагается что фермент E имеет по крайней мере три каталитических центра, способных одновременно фиксировать две молекулы X и одну молекулу Y . Если образующиеся комплексы распадаются с достаточно большой скоростью, а ферменты присутствуют в небольших количествах, легко показать, что всю последовательность реакций можно свести к одной стадии, дающей нелинейный член типа X 2 Y в выражении для скорости реакции.

Брюсселятор представляет собой следующую схему гипотетических химических реакций:

Здесь А , В - исходные вещества, C , R - продукты, X , Y - промежуточные вещества.

Пусть конечные продукты С и R немедленно удаляются из реакционного пространства. Это означает, что обратные константы k - 3 = k - 4 = 0. Если субстрат A находится в избытке, k - 1 = 0. Предположим также, что k - 2 = 0. Значения остальных констант положим равными единице. Тогда схема реакций 9.2 (в случае точечной системы) описывается системой уравнений:

,

Модель (8.5) имеет одну особую точку с координатами:

. (8.7)

Исследуем стационарное решение (8.6) на устойчивость по методу Ляпунова. Введем переменные, характеризующие отклонения от особой точки:

Линеаризованная система имеет вид:

,

.

Характеристическое уравнение

l 2 + (A 2 + 1 - B ) l + A 2 = 0

имеет корни:

Напомним, что особая точка является устойчивой, если действительные части корней характеристического уравнения отрицательны. Из выражения (8.7) видно, что при B < 1+ A 2 особая точка (8.6) устойчива. Если же B > 1 + A 2 особая точка становится неустойчивой, и у системы (8.5) появляется устойчивый предельный цикл. Значение B =1+ A 2 является бифуркационным. Если величина B лишь немного превосходит бифуркационный порог, автоколебания в системе носят квазигармонический характер. Таким образом, брюсселятор при выполнении условия

B > 1 + A 2 (8.8)

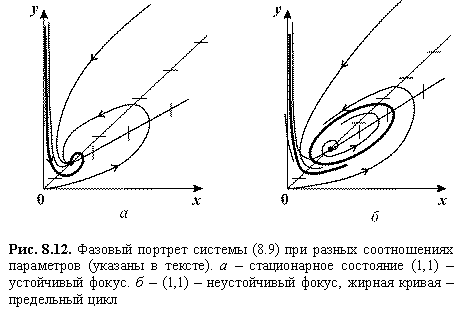
является автоколебательной системой. Фазовый портрет брюсселятора при разных значениях параметров изображен на рис. 8.9

Здесь мы приведем краткий обзор нескольких «успешных» моделей колебательных биологических процессов. Более подробно некоторые колебательные процессы будут рассмотрены в лекциях 9, 11, 12.

Модель темновых процессов фотосинтеза.

Одной из первых моделей, описывающих колебательный процесс в живой системе, была модель темновых процессов фотосинтеза, предложенная и исследованная Д.С.Чернавским с сотрудниками (1967). Модель является примером системы второго порядка с квадратичными правыми частями, в которой возникают автоколебания (существует предельный цикл) и допускает полное аналитической исследование (Белюстина, 1967)

Известно, что в условиях смены дня и ночи интенсивность фотосинтеза, то есть скорость выделения кислорода и поглощения СО 2 изменяется периодически (рис.8.10 а ). Если растение поместить в условия непрерывной освещенности, то периодичность в интенсивности фотосинтеза с периодом несколько часов сохраняется достаточно длительное время. По-видимому, растение имеет свой внутренний ритм, синхронизованный с периодическим внешним воздействием.

Напомним, что в процесс фотосинтеза входят световой и темновой циклы химических реакций. Первый включает поглощение энергии квантов света и, через ряд промежуточных стадий, приводит к образованию высокоэнергетических восстановленных химических соединений и богатых энергией молекул АТФ. Эти вещества употребляются в темновом цикле (цикле Кальвина), в котором свет непосредственно не участвует. Здесь происходит восстановление углекислоты СО 2 с помощью веществ, богатых энергией, и доноров водорода, полученных в световом цикле, и превращение ее в углеводы ‑ фруктозу и глюкозу (рис. 8.11).

В цикле участвуют углеводы с различным содержанием углерода (индекс внизу означает число атомов углевода в молекуле). Все трехуглеродные сахара имеют общее названиетриозы (с 3 ), пятиуглеродные (с 5 ) ‑ пентозы, шестиуглеродные (с 6 ) ‑ гексозы. Цикл замкнут, т.е. вещество, к которому первоначально присоединяется углекислота (акцептор СО 2 , обозначенный на рис. 8.8 символом с 5 ) в результате реакции регенерируется. Самые простые сахара ‑ триозы ‑ непосредственно связаны со световым циклом, остальные сахара со световым циклом не связаны. Все реакции в цикле, за исключением первичной фиксации СО 2 на рибулезе, бимолекулярные, и зависимость скорости реакции от концентрации описывается членами второго порядка.

Для упрощения системы были выделены группы веществ, реакции между которыми протекают быстро и обратимо, легкие сахара (трехуглеродистые углеводы) и более тяжелые шестиуглеродные сахара. Суммарная концентрация первых обозначалась условно с 3 , а вторых с 6 .

Предполагалось, что прибыль тяжелых сахаров с 6 может осуществляться за счет соединения двух легких с 3 . Их убыль, так же как и убыль тяжелых сахаров, происходит в результате бимолекулярного взаимодействия тяжелых и легких сахаров. Имеет место также приток продукта с 3 в сферу реакции за счет биохимически сходных процессов (гликолиза, дыхания). Эти предположения приводят к системе уравнений:

(8.9)

Переменные представляют собой нормированные концентрации легких (x ) и тяжелых (y ) сахаров. В положительном квадранте имеется одно состояние равновесия с координатами (1,1). Изоклины горизонтальных касательных определяются из уравнения

а изоклины вертикальных касательных – из уравнения

На рис. 8.12 изображены фазовые портреты системы. При это устойчивый фокус (рис. 8.12 а ). При - неустойчивый фокус, окруженный предельным циклом (рис. 8.12 б ).

Колебания в гликолизе.

Классическим примером колебательной биохимической реакции является гликолиз. В процессе гликолиза осуществляется распад глюкозы и других сахаров, при этом соединения, содержащие шесть молекул углерода, превращаются в трикарбоновые кислоты, включающие три молекулы углерода. За счет избытка свободной энергии в процессе гликолиза на одну молекулу шестиуглеродного сахара образуются две молекулы АТФ. Основную роль в генерации наблюдаемых колебаний концентраций компонентов реакции: фруктозо-6-фосфата, фруктозо-1,6-фосфата и восстановленного НАД (никотинаминадениндинуклеотид ) играет ключевой фермент гликолитического пути - фосфофруктокиназа (ФФК). Упрощенная схема реакций представлена на рис. 8.13:

На схеме [Гл] - глюкоза, Ф6Ф - фруктозо-6-фосфат - субстрат ключевой реакции, ФДФ ‑ продукт этой реакции, который является субстратом в следующей стадии. Обе реакции катализируются ферментами. В безразмерных переменных система описывающих реакции уравнений может быть записана в виде:

Здесь зависимости скоростей реакций от переменных записаны в форме Михаэлиса-Ментен (Моно), как это было представлено в уравнении (8.10).Если выполняются условия: K mx >> x , K my >> y , можно произвести замену переменных 8.14

Рис. 8.14. х ) и фруктозодифосфата (у а ‑ бесколебательный процесс (узел на фазовой плоскости), α = 0.25; r = 1. б –затухающие колебания (устойчивый фокус на фазовой плоскости) α = 4; r = 0.2

Рис. 8.14. Модель гликолиза (8.10). Кинетика изменений концентраций фруктозо‑6‑фосфата (х ) и фруктозодифосфата (у ) (справа) и фазовый портрет системы (слева) при разных значениях параметров системы, в – колебания с постоянной амплитудой и фазой, близкие к гармоническим (предельный цикл на фазовой плоскости), α = 6; r = 0.2. г – релаксационные колебания с постоянной амплитудой и фазой, (предельный цикл почти треугольной формы на фазовой плоскости) α = 8; r = 0.5

Интересно, что колебательные реакции в системе гликолиза были сначала предсказаны на математической модели (Higgins, 1964), и лишь после этого зарегистрированы экспериментально с помощью метода дифференциальной спектрофотометрии в лаборатории Б.Чанса (1966).

Внутриклеточные колебания кальция .

Во многих типах живых клеток наблюдаются колебания внутриклеточной концентрации кальция, период которых может варьировать от 0,5 до 10 мин. Простейшая схема процессов, приводящих к гармонально обусловленным колебаниям кальция, основой которых служит кальций индуцированный выходакальция из клетки, приведена на рис. 8.15. Такие колебания впервые наблюдались Эндо с соавторами (1970) на клетках скелетных мышц, Фабиато (1975) на клетках саркоплазматического ретикулума сердца быка, и позднее - многими другими исследователями.

Схема и модель процессов, предложена и оп исана в . Рассматриваются приток и отток кальция в клетку через плазматическую мембрану (константы скоростей v 1 и v 2 , соответственно); гормонально активируемое освобождение кальция из пула (скорость v 3 ); активный транспорт цитозольного кальция в пул, (v 4 ), освобождение кальция из пула, активируемое цитозольным кальцием (v 5 ); свободный отток кальция из пула в цитозоль (v 6 ). Модель состоит из двух дифференциальных уравнений

(8.11)

Клеточные циклы.

В процессе жизненного цикла клетка удваивает свое содержимое и делится на две. В организме млекопитающего для поддержания жизни производятся ежесекундно миллионы новых клеток. Нарушение регуляции пролиферации клеток проявляется как онкологическое заболевание. Этим вызван большой интерес к изучению и моделированию механизмов регуляции клеточного деления.

Схема клеточного цикла изображена на рис. 8.17. Клеточный цикл состоит из двух периодов: митоз (М ‑фаза) включает разделение предварительно удвоенного ядерного материала, деление ядра и деление самой клетки ‑ цитокинез и занимает около часа. Значительно более длительный период между двумя митозами занимает интерфаза, включающая стадию роста G 1 , фазу репликации ДНК (S ), фазу подготовки к делению G 2 . Клеточный цикл (рис.8.17) регулируется генами и белками-ферментами двух основных классов.

Циклин-зависимые протеин‑киназы (Cdk) индуцируют последовательность процессов путем фосфорилирования отдельных белков. Циклины, которые синтезируются и деградируют при каждом новом цикле деления, связываются с молекулами Cdk и контролируют их способность к фосфорилированию, без циклина Cdkне активны. Количество этих молекул‑регуляторов различно в разного вида клетках.

В делении дрожжевой клетки основные роли играют один Cdk и девять циклинов, которые образуют девять разных циклин‑Cdk комплексов. У гораздо более сложно организованных млекопитающих изучено шесть Cdk и полтора десятка циклинов. Контроль выхода клетки из G 1 , и G 2 фаз осуществляют промотор‑фактор S‑ фазы (SPF) и промотор‑фактор M ‑фазы (MPF), представляющие собой гетеродимеры. Cуществует особая контрольная точка клеточного цикла (Start), с которой заканчивается рост (G 1 фаза) и начинается процесс синтеза ДНК.

Простая модель процесса предложена Тайсоном (Tyson, 1995). Постулируется существование фактора транскрипции SBF, который может быть в активной S a и пассивной S i форме. Он переходит в активную форму под действием циклина Cln (N ) и Start‑киназы (Cdc28-Cln3) (A ) и инактивируется другим веществом (Е ). Циклин продуцируется путем активации SBF и деградирует. SBF активируется Chu и Start-киназой и инактивируется фосфатазой. Безразмерная модель процессов имеет вид:

(8.13)

Модель имеет одно или три стационарных решения (два устойчивых) в зависимости от значений параметров, и при увеличении параметра a (в процессе роста клетки) описывает переключение системы из G 1 в S фазу.

Добавление двух уравнений сходного вида позволяет описать также переключение из G 2 в фазу митоза М . Полная модель, учитывающая и другие регуляторные ферменты в фосфорилированной и дефосфорилированной форме содержит 9 нелинейных уравнений (Novak, Tyson 1993) и хорошо описывает кинетику деления ооцитов Xenopus . При соответствующем подборе параметров она применима к описанию деления других типов клеток.

Большое количество работ было посвящено попыткам моделирования периодического воздействия на клеточный цикл с целью оптимизации параметров рентгено‑ радио‑ или хемотерапии при воздействии на клетки онкологических опухолей.

В современной литературе по математической биологии рассмотрены сотни автоколебательных систем на разных уровнях организации живой природы. Несомненно, колебательный характер процессов - эволюционное изобретение природы, и их функциональная роль имеет несколько разных аспектов.

Во-первых колебания позволяют разделить процессы во времени, когда в одном компартменте клетки протекает сразу несколько различных реакций, организуя периоды высокой и низкой активности отдельных метаболитов. Во-вторых, характеристики колебаний, их амплитуда и фаза, несут определенную информацию и могут играть регуляторную роль в каскадах процессов, проходящих на уровне клетки и живого организма. Наконец, колебательные (потенциально или реально) системы служат локальными элементами распределенных активных сред, способных к пространственно‑временной самоорганизации, в том числе к процессам морфогенеза. Эту роль колебательных систем мы подробно рассмотрим во второй части лекций.

Литература

Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., Наука, 1981.

Белюстина Л.Н., Кокина Г.А. Качественное исследовани е уравнений фотосинтеза. – В сб. Колебательные процессы в биологических и химических системах. М., Наука, 1967

Гленсдорф П., Пригожин И. Термодинамическая теория структуры, стабильности и флуктуаций. М., 1978

Николис Ж, Пригожин И. Самоорганизация в неравновесных системах. М., Мир., 1979

Чернавский Д.С., Чернавская Н.М. О колебаниях в темновых реакциях фотосинтеза. – В сб. Колебательные процессы в биологических и химических системах. М ., Наука , 1967

Dupont G. and Goldbetter A. Theoretical insights into the origin of signal-induced calcium oscillations, in Goldbeter A. (ed). Cell to Cell signalling: From experiments to theoretical models. Acad. Press, London, pp. 461-474, 1989

Dupont G. and Goldbetter A. Oscillations and waves of citosolic calsium: insights from theoretical models. Bioessays, 14, 485-493, 1992

Higgins J.A. A chemical mechanism for oscillations in glicolitic intermediates in yeast cells. Proc. Nat. Acad. Sci. USA, v.51, 1954

Higgins J.A. The theory of oscillating reactions. Ing. Chem. V.59, N5, 1967

Hopf E. Abzweilung einer periodischen Losung von einer stationaren Losung eines Differentialsystems (bifurcation of a periodic solusion from stationary solution of a system of differential equations) Ber. Math-phys. Kl. Sachs. Akad. Wiss. Leipzig 94, 3-22, 1942

Novak B, Tyson J.J. Modeling the cell division cycle: M-phase trigger, oscillation and size control, J. Theor. Biol. 165, 101-104, 1993

Somogyi R, Stuckin J.W. Hormone-induced calcium oscillations in liver cells can be explainedby a simple one pool model. J. Biol. Chem.266, 11068-11077, 1991

Prigozhine I.R., Lefebre R. Simmetry breaking instabilities indissipative systems.J. Che. Phys., 48, 1665-1700, 1968

Winfree A.T. The Geometry of Biological Time. Springer, 1980

Которой нет других периодических траекторий. Эквивалентным является утверждение, что всякая достаточно близкая к предельному циклу траектория стремится к нему либо в прямом, либо в обратном времени.

Катастрофа голубого неба

Однако, на бутылке Клейна или при рассмотрении комплексифицированных предельных циклов, возможна и более сложная бифуркация - так называемая катастрофа голубого неба . А именно, при стремлении параметра к критическому значению длина (одного!) предельного цикла начинает нарастать, стремясь к бесконечности, и поэтому он не продолжается на сам момент бифуркации.

Физический пример: осциллятор Ван дер Поля

• Van der Pol oscillator в Scholarpedia.

16-я проблема Гильберта

Вторая часть 16-й проблемы Гильберта касается возможного количества и расположения предельных циклов векторных полей на плоскости. В отличие от первой - алгебраической - части, требующей описать расположение овалов алгебраической кривой заданной степени, даже для квадратичных векторных полей неизвестно существование равномерной оценки сверху на число предельных циклов.

См. также

• Гипотеза Аносова

Литература

• А. Б. Каток, Б. Хасселблат Введение в современную теорию динамических систем с обзором последних достижений / пер. с англ. под ред. А. С. Городецкого. - М .: МЦНМО, 2005. - 464 с. - ISBN 5-94057-063-1
• Ю. С. Ильяшенко, Динамические системы и философия общности положения, М.:МЦНМО, 2007, ISBN 978-5-94057-353-1
• Yu. Ilyashenko, Centennial history of Hilbert 16th problem, Bull. Amer. Math. Soc. 39 (2002), 301-354

Wikimedia Foundation . 2010 .

• Предельные монокарбоновые кислоты
• Предзародышевое развитие

Смотреть что такое "Предельный цикл" в других словарях:

ПРЕДЕЛЬНЫЙ ЦИКЛ - замкнутая изолированная траектория в фазовом пространстве динамич. системы, изображающая периодич. движение. В окрестности П. ц. фазовые траектории либо удаляются от него (неустойчивый П. ц.), либо неограниченно приближаются к нему «наматываются» … Физическая энциклопедия

предельный цикл - — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN limit cyclelimiting cycle … Справочник технического переводчика

Предельный цикл - системы дифференциальный уравнений 2 го порядка замкнутая траектория в фазовом пространстве xOy, обладающая тем свойством, что все траектории, начинающиеся в достаточно узкой кольцеобразной ее окрестности, неограниченно… … Большая советская энциклопедия

ПРЕДЕЛЬНЫЙ ЦИКЛ - замкнутая траектория в фазовом пространстве автономной системы обыкновенных дифференциальных уравнений, к рая является a или w предельным множеством (см. Предельное множество траектории) хотя бы для одной другой траектории этой системы. П. ц. наз … Математическая энциклопедия

предельный цикл - ribinis ciklas statusas T sritis automatika atitikmenys: angl. limit cycle vok. Grenzschwingung, f; Grenzzyklus, m rus. предельный цикл, m pranc. cycle limite, m … Automatikos terminų žodynas

Экономический словарь

предельная петля гистерезиса - предельный цикл гистерезиса; предельная петля гистерезиса Наибольший по площади цикл гистерезиса магнитного материала … Политехнический терминологический толковый словарь

При анализе шума округления в цифровых фильтрах предполагалось, что разность между соседними отсчетами входного сигнала велика по сравнению с шагом квантования. Это позволяло считать, что отсчеты шума округления некоррелированы как друг с другом, так и с отсчетами входной последовательности. Ясно, что во многих случаях (например, если входной сигнал постоянен или равен нулю) такое предположение несправедливо.

Рассмотрим в качестве примера разностное уравнение

и предположим, что входная последовательность (т. е. вход фильтра отключен), а начальное условие имеет вид (Значения переменной у выражаются в единицах шага квантования Q и поэтому не могут быть дробными.) В приводимой ниже таблице сопоставляются точные значения , рассчитанные, согласно уравнению (5.122), без использования округления, а также значения, получающиеся при расчетах с округлением.

Хотя точные значения экспоненциально стремятся к нулю, при использовании округления значения «затягиваются» на уровне, равном 10, и дальше уже не могут измениться. Рассмотренный пример иллюстрирует возникновение в рекурсивном цифровом фильтре эффекта предельного цикла при нулевом входном сигнале. Амплитудные интервалы, в которых возникают эффекты предельного цикла, Блэкман назвал мертвыми зонами. В рассмотренном примере при любом будет получаться, что , если . Таким образом, интервал является мертвой зоной.

Джексон исследовал предельные циклы в системах первого и второго порядка, используя понятие «эффективных значений» коэффициентов фильтра, т. е. учитывая, что предельные циклы возникают только тогда, когда округление фактически приводит к появлению полюсов на единичной окружности. Так, для системы, описываемой разностным уравнением первого порядка

где символ обозначает операцию округления до ближайшего целого, а при , мертвой зоной, в которой могут существовать предельные циклы, является интервал , причем к равно наибольшему целому числу, удовлетворяющему неравенству

(5.124)

Из приведенного примера следует, что при отрицательных а отсчеты на выходе фильтра в режиме предельного цикла имеют постоянные амплитуду и знак. Если же , то отсчеты на выходе в режиме предельного цикла будут иметь постоянную амплитуду, но чередующийся знак. При всех значениях в пределах мертвой зоны эффективное значение множителя а равно ±1, т. е. . Таким образом, разностному уравнению (5.123) соответствует эффективный полюс в точке .

Для системы второго порядка, описываемой разностным уравнением

мертвой зоной, в которой могут возникать эффекты предельного цикла, является интервал , где k - наибольшее целое, удовлетворяющее неравенству

(5.126)

Формула (5.126) аналогична формуле (5.124), но а заменено на . При выполнении соотношения (5.126) полюсы фильтра наверняка попадают на единичную окружность, т. е. эффективное значение равно 1,0. (Отметим, что при полюсы будут комплексно сопряженными, а фильтр - устойчивым.) Частота колебаний в режиме предельного цикла определяется главным образом значением но зависит также и от того, как округление сказывается на величине произведения в формуле (5.125).

Из формулы (5.126) следует, что наименьшее значение при котором еще образуется пара эффективных комплексно сопряженных полюсов равно 0,5. В этом случае Следующее значение для которого эффекты предельного цикла возникают при большем значении k, равно 0,75. В этом случае или 2. При любом значении существует только конечное число интервалов значений , при которых могут возникать различные эффекты предельного цикла. Соответствующие области в плоскости для блока второго порядка, описываемого уравнением (5.125), показаны на фиг. 5.42. Область, в которой предельные циклы не возникают, отмечена штриховкой. Горизонтальные линии соответствуют минимальным значениям , при которых происходит изменение режима в мертвой зоне. Числа внутри каждой из областей обозначают максимальное значение амплитуды колебаний в режиме предельного цикла, возможных в этой области плоскости .

Фиг. 5.42. Зависимость амплитуды колебаний предельного цикла от коэффициентов фильтра (по Джексону).

Предельные циклы, возникающие при , будут рассмотрены ниже.

Выше были проанализированы эффекты предельного цикла в блоках второго порядка, соответствующие возникновению пары эффективных комплексно сопряженных полюсов. Предельные циклы в таких блоках могут существовать и при появлении действительного эффективного полюса в точке z = ±1. В этом случае условием возникновения режима предельного цикла с выходной амплитудой, равной к, является следующее равенство:

Для различных значений к нетрудно определить положение областей в плоскости , внутри которых выполняется условие (5.127). Эти области показаны на фиг. 5.42.

Изучение предельных циклов важно по двум причинам. В системах связи отключение сигнала может вызвать эффекты предельного цикла. Это весьма нежелательно, поскольку хотелось бы, чтобы при отсутствии входного сигнала на выходе канала ничего не было слышно. Поэтому при использовании цифровых фильтров в системах телефонии данной проблеме следует уделить достаточно серьезное внимание. Вторая причина заключается в том, что предельные циклы можно использовать для генерации периодических последовательностей. Колебания предельного цикла с нужными характеристиками можно использовать при цифровой обработке в качестве источника сигнала.

После выхода в свет работы Джексона, посвященной предельным циклам, уточнению границ для амплитуд и частот колебаний предельного цикла уделялось очень много внимания. Подробности можно найти в соответствующих публикациях.

ЛИТЕРАТУРА

Литература общего характера

1. Oppenheim А. V., Weinstein С. W., Effects of Finite Register Length in Digital Filters and the Fast Fourier Transform, Proc. IEEE, 60, No. 8, 957-976 (Aug. 1972); есть русский перевод: Оппенгейм, Вайнштейн, Влияние конечной длины регистра при цифровой фильтрации и быстром преобразовании Фурье, ТИИЭР, т. 60, № 8, стр. 41-65 (1972).

2. Gold В., Rader С. М., Digital Processing of Signals, Ch. 4, McGraw-Hill, 1969; есть русский перевод: Голд Б., Рэйдер Ч., Цифровая обработка сигналов, изд-во «Советское радио», 1973.

3. Liu В., Effect of Finite Word Length on the Accuracy of Digital Filters - A Review, IEEE Trans. Circuit Theory, CT-18, 670-677 (Nov. 1971).

4. Bennett W. R., Spectra of Quantized Signals, Bell Syst. Tech. J., 27, 446- 472 (July 1948).

5. Rader С. M., Gold В., Effects of Parameter Quantization on the Poles of a Digital Filter, Proc. IEEE, 55, No. 5, 688-689 (May 1967); есть русский перевод: Рейдер, Голд, Влияние квантования параметров на полюсы цифрового фильтра, ТИИЭР, 55, № 55, стр. 98-100 (1967).

Шум округления в рекурсивных структурах. Случай фиксированной запятой

1. Knowles J. В., Edwards R., Effects of a Finite-Word-Length Computer in a Sainpled-Data Feedback System, Proc. Inst. Elec. Eng., 112, 1197- 1207 (June 1965).

2. Gold В., Rader С. M., Effects of Quantization Noise in Digital Filters, Proc. AFIPS 1966 Spring Joint Computer Conf., 28, 213-219 (1966).

3. Jackson L. В., On the Interaction of Roundoff Noise and Dynamic Range in Digital Filters, Bell Syst. Tech. J., 49, 159-184 (Feb. 1970).

4. Jackson L. В., Roundoff Noise Analysis for Fixed-Point Digital Filters Realized in Cascade or Parallel Form, IEEE Trans, on Audio and Electro-acoustics, AU-18, 107-122 (June 1970).

Шум округленна в нерекурсивных структурах. Случай фиксированной запятой

1. Chan D. S. К., Rabiner L. R., Theory of Roundoff Noise in Cascade Realizations of Finite Impulse Response Digital Filters, Bell Syst. Tech. J., 52, No. 3, 329-345 (March 1973).

2. Chan D. S. K., Rabiner L. R., An Algorithm for Minimizing Roundoff Noise in Cascade Realizations of Finite Impulse Response Digital Filters, Bell Syst. Tech. J., 52, No. 3, 347-385 (March 1973).

3. Chan D. S. K., Rabiner L. R., Analysis of Quantization Errors in the Direct Form for Finite Impulse Response Digital Filters, IEEE Trans, on Audio and Electroacoustics, AU-21, No. 4, 354-366 (Aug. 1973).

Шум округления в рекурсивных структурах. Случай плавающей запятой

1. Sandberg I. W., Floating-Point Roundoff Accumulation in Digital Filter Realization, Bell Syst. Tech. J., 46, 1775-1791 (Oct. 1967).

2. Капеко Т., Liu В., Roundoff Error of Floating-Point Digital Filters, Proc. Ш Annual Allerton Conf. on Circuit and System Theory, 219-227 (Oct. 1968).

3. Weinstein C., Oppenheim A. V., A Comparison of Roundoff Noise in Floating Point and Fixed Point Digital Filter Realizations, Proc. IEEE (Corresp.), 57, 1181-1183 (June 1969); есть русский перевод: Вайнштепн, Оппенгейм, Сравнение шумов округления цифровых фильтров при пх реализации по методу с плавающей запятой и по методу с фиксированной запятой, ТИИЭР, т. 57, № 7. стр. 72-74 (1969).

4. Liu В., Капеко Т., Error Analysis of Digital Filters with Floating-Point Arithmetic, Proc. IEEE, 57, 1735-1747 (Oct. 1969); есть русский перевод: Лиу, Канеко, Анализ погрешностей цифровых фильтров, реализуемых арифметическими операциями с плавающей запятой, ТИИЭР, т. 57, № 10, стр. 49-63 (1969).

5. Oppenheim А. V., Realization of Digital Filters Using Block Floating-Point Arithmetic, IEEE Trans, on Audio and Electroacoustics, AU-18, 130-136 (June 1970).

Колебания переполнения

1. Ebert P. M., Mazo J. E., Taylor M. G., Overflow Oscillations in Digital Filters, Bell Syst. Tech. J., 48, 3021-3030 (Nov. 1968).

Квантование коэффициентов в рекурсивных структурах

2. Kaiser J. F., Some Practical Considerations in the Realization od Linear Digital Filters, Proc. 3rd Annual Allerton Conf. on Circuit and System Theory, 621 - 633 (1965).

3. Rader С. M., Gold В., Effects of Parameter Quantization on the Poles of a Digital Filter, Proc. IEEE (Corresp.), 55, 688-689 (May 1967).

4. Knowles J. В., Olcayto E. M., Coefficient Accuracy and Digital Filter Response, IEEE Trans. Circuit Theory, 15, No. 1, 31-41 (March 1968).

5. Avenhaus E., Schuessler H. W., On the Approximation Problem in the Design of Digital Filters with Limited Wordlength, Arch. Elek. Ubertragung, 24, 571-572 (1970).

Квантование коэффициентов в нерекурсивных структурах

1. Hermann О., Schuessler Н. W., On the Accuracy Problem in the Design of Nonrecursive Digital Filters, Arch. Elek. Ubertragung, 24, 525-526 (1970).

2. Chan D. S. K., Rabiner L. R., Analysis of Quantization Errors in the Direct Form for Finite Impulse Response Digital Filters, IEEE Trans, on Audio and Electroacoustics, AU-21, No. 4, 354-366 (Aug. 1973).

3. Weinstein C. W., Quantization Effects in Frequency Sampling Filters, NEREM Record, 22 (1968).

Предельные циклы в рекурсивных структурах

1. Blackman R. В., Linear Data-Smoothing and Prediction in Theory and Practice, Addison-Wesley Puhl. Co., Reading, Mass., pp. 75-79 (1965).

2. Jackson L. В., An Analysis of Limit Cycles Due to Multiplication Rounding in Recursive Digital (Sub) Filters, Proc. 1th Annual Allerton Conf. on Circuit and System Theory, 69-78 (1969).

3. Parker S. R., Hess S. F., Limit-Cycle Oscillations in Digital Filters, IEEE Trans. Circuit Theory, CT-18, 687-696 (Nov. 1971).

4. Sandberg I. W., A Theory Concerning Limit Cycles in Digital Filters, Proc. 7th Allerton Conf. on Circuit and System Theory, 63-67 (1969).

5. Brubaker T. A., Gowdy J. N., Limit Cycles in Digital Filters, IEEE Trans. Automatic Control, 17, No. 5, 675-677 (Oct. 1972).

6. Sandberg 1. W., Kaiser J. F., A Bound on Limit Cycles in Fixed-Point Implementations of Digital Filters, IEEE Trans, on Audio and Electroacoustics, AU-20, No. 2, 110-112 (June 1972).